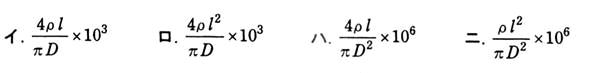
よく出る上に簡単な問題。一番最初に勉強すべき内容。
問題分では電線など、細長い導体の抵抗に問う問題群になっている
素材や単位がでてきて見るからに難しい。
しかしそれらはすべて無視して、長さ、直径、断面積だけで問題が解ける
導体とは電流を流す物体のこと。電線でも銅線でも、電流を流すものはなんでも導体と呼ぶ。
導線とか電線と呼ばれたりもするが、全部同じ意味だと思ってよい
これは当サイト記念すべき最初の問題である。
前知識なしで、問題文を読んでも、意味がわからんだろう。
ヒントは一つだけだす。
電線に大量に電流を流すと、それだけ高温になり危険である
それぐらい知ってるって?ではフィーリングでこの問題を正解してもらいたい。
はい。じゃ、どれが一番誤ってると思った?
つまり正解は、ハである。
許容電流は、周囲の温度が上昇すると、大きくなる?
え、そうなの?むしろ逆っぽい気がする・・・許容電力ってなに?
そんな感じでハが怪しいと気づくだろう。
許容電力とはその名の通り、電線などの導体に、流しても安全な電流の量である
この許容電力がなぜ定められているか、というと、
電線に際限なく電流を流すと、高温になりすぎて危険だからである
導体である電線部分や、電線を包むゴムの絶縁体が焼け解けてしまうのだ
だから導体や周囲が高温であれば、それだけ流す電力の量は少なくしなければ危険である。
読みかえると、許容電流は、周囲の温度が上昇すると、小さくしなければならない。
以下は問題の詳しい解説だが、面倒なので読まなくてよい。
まず問題文を次のように簡略化できる
導体の抵抗の公式により、抵抗は、電線が長くなると増加し、太くなると減少する。
太くなるとは直径が増加することである。
つまり、イとロは正であり、解答ではない。
ハとニの解答は許容電流についてしる必要がある
電線などの導体は電気を流すと、熱を発生する
これは電線の抵抗が、流れる電流を熱に変換しているためである
つまり抵抗が大きいほど、電流は失われ、多くの熱を発生させてしまう
そして大量の電気を流すと、高温になりすぎて、導体(電線)が焼き解けてしまう
そのため流せる電流は、電線の材料と形状による抵抗値によって上限が定められている。
それが許容電流である。き
もちろん許容電流を超えた電流を流すと高温になりすぎて非常に危険である
以上から抵抗が小さいほど、熱が発生しづらくなり、許容電流の数値は大きくなる。
つまりニの、「許容電流は、直径が大きくなると、大きくなる」は正である。
これらから、消去法によって、誤っているのは、ハであるとわかる。
詳しく知らなくても、電線は大きな電流を流すと、熱を発生する。周囲が高温なら余計に熱くなる。
そのため許容電力を小さくしなければならない。許容電流をしらなくても、イメージで回答できるかもしれない。
直接ハが間違っていると知るには、許容電力と導体の温度変化による抵抗の増加を知る必要がある。
金属などの導体は温度が上がると、より抵抗が増していく。
導体の抵抗が大きくなると、それを通る電流が抵抗によって熱に変わる
つまり周囲が高温だと、電流を流した導体はより高温になる
一方導体の許容電流は、導体の温度が上がりすぎないように制限するもの
この状態では許容電量を下げなければならない。
つまり許容電流は、周囲の温度が上昇すると、大きくなるが間違っているとわかる。
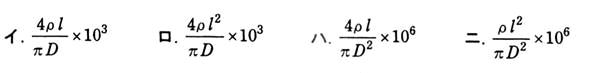
これは導体の電気抵抗の公式を理解しているか問う問題である
"導体 電気抵抗"でググれば、解答がわかる
わけない
導体の電気抵抗式がいくつもあり。
さらに使われている単位について理解しなければさっぱりわからない。
この問題は見た目よりずっと難しく、理解するのは時間の無駄である
問題理解ではなく、答えの見つけ方を紹介する
この問題と解答文を覚えておく。
解答4つに記号が多用され、特徴的なので、理解できなくてもすぐに見分けられる
そして解答の×10^3と×10^6を見つける
この場合、×10^6とついているほうが正解で、ハとニに正解を絞り込める
次に、4ρLと書いてあるハが正解である。
答えがハだとわかり、見つけ方もわかったので、これ以上考えるのは時間の無駄
不要だが、以下問題の解説をする
×10^6について解説する。
問題文の直径Dが[mm](ミリメートル)単位で、これを[m]メートルに直さなければならない
メートルはミリメートルの1000倍なので×1000。つまり×10^3と表記する
しかし、×10^3が記載された、イとロを選ぶのは誤りである。
導体の断面積を求めるために、半径を二乗する。
よくわからんが、1000^2=100000=×10^6が導き出せる
そして正解は4ρLとついているハである。
この4は断面積を求める式(半径×半径×3.14)の、1/2直径×1/2直径があり。計算すると1/4となる。
この4は、その1/4のことである。意味わからんだろ?
この問題は難しいので、詳しく考えるのをやめて
×10^6と4ρLが付いてるのが正解だと記憶しろ
[m]、[mm]、[mm^2]と三つの単位が出てきて混乱するが、無視してよい
この導線の直径2,6を使って、円柱の断面積を求めると正解がわかる
導線の断面積=1.3(半径)×1.3(半径)×3.14(円周率)=5.3066
ぶっちゃけ5.3でよい。4択だから。
つまり問題の導線は、断面積5.3[mm^2]、長さ10[m]である
ロの断面積5.5[mm^2]、長さ10[m]の導線が一番近い
長さが2倍になると、電線の抵抗は2倍になる
直径が2倍になると、断面積は4倍になり、抵抗は1/4になる
抵抗を比べるなら、本来であれば円柱の断面積を比較するため、半径*半径*3.14を計算しなければならない
しかし直径が2倍なら、断面積は4倍になり
つまり抵抗は1/4になるとわかる。
Aの導線の直径1.6は、Bの直径3.2の1/2。断面積は1/4となり、抵抗は4倍となる
Aの長さ100はBの長さ50の2倍なので、抵抗は2倍
よって4*2で、Aの抵抗はBの8倍だということが分かる
上とほとんど同じ問題だが、Aは細くて短い、Bは太くて長いため、やや難易度が上がっている。
Aの導線の直径1.6は、B直径3.2の1/2。Aの断面積はBの1/4となる。
断面積を比較すると、Aの抵抗は、抵抗は4倍となる
Aの長さ20は、Bの長さ40mの1/2。
長さを比較するとAの抵抗はBの1/2である
4*1/2=2。Aの抵抗はBの2倍であることが分かる。
Aの直径はBの1/2であり、断面積は1/4倍となる。つまり抵抗は4倍。一方長さが2倍なので抵抗は2倍となる 2倍が正解

導体(導線)とは電気を流せる物体のことで電線などのこと
導体(電線)の電気抵抗R、導体の断面積をA、導体の直径をD、長さをLとする
アルファベットに置き換えるのはわかりづらいが、問題文でよくつかってくるので、慣れていたほうが問題は解きやすい
電線の素材は銅やアルミなど電流を通しやすい素材だが、わずかな抵抗がある
そのため電線が長くなるほど、それを通る電流は多くの抵抗にさらされる。
よって電線の長さLが大きいほど、抵抗は大きい
電線などの導線は長さLが二倍になると、抵抗も2倍になる
=導線の抵抗(R)は、長さ[L]に比例
道や水と同じで、電線が太いほうが、その中を通る電流は進みやすい
電流が進みやすい=抵抗が小さい=電線が太いほど、抵抗は小さい
電線の太さは、電線の直径(D)かであらわされる。
つまり電線の直径(D)が大きいほど、抵抗は小さい
直径と同じく、導体の太さは、断面積であらわされる。
つまり断面積が大きいほど、抵抗は小さくなる=導体の抵抗(R)は、断面積(A)に反比例
導線の直径が倍になると、電線の断面積は4倍になる。よって抵抗は4分の一になる
これは二つの導線の抵抗を比較する問題を解くのに利用する
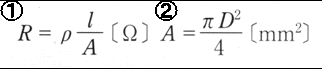
導線の直径から、断面積を求めないと解けない問題が出題される
電線のような導線(導体)は、円柱形なので、断面積は算数の半径×半径×3.14で求められる。
導線の断面積をA、直径をD、円周率をπ、単位を[mm^2](ミリ平方メートルとおくと)断面積Aは以下の式であらわされる
A=1/2D×1/2D×π×[mm^2]=1/4×D^2×10^6=(D^2π)/4×10^6
Rを電気抵抗、抵抗率をρ、導体の長さをL、導体の断面積をAとおく
R(電気抵抗)=(ρ×L)/A[Ω]
抵抗率ρ〔Ω・m〕、直径D〔mm〕、長さL〔m〕の導線の電気抵抗を表す式は。